Dipole Antennas - the Effect of Height Above Ground
I frequently hear the question: how high should my dipole be? Or alternatively, will my dipole work well at this or that height? Unfortunately, these questions can not be answered without first stating what you want the dipole to actually DO, i.e. how you plan to operate with it. Some possible goals for a dipole might be:
1. DX work.
2. Local work: nets and rag chewing.
3. Directionality: gain in one direction, or nulls in some other direction
4. Omni-directionality.
5. Feed point impedance of 50 ohms.
As you may surmise, many of these potential goals are mutually exclusive, or at least tradeoffs.
However, once you define what you want to do with your dipole, then you can look at the radiation patterns to see if it will accomplish those goals.
I make the assumption that anyone reading this understands that DX work requires a low angle of radiation, with gain in the favored direction being desirable. Nets and rag chewing require a much higher angle of radiation and an omni-directional pattern. A null aimed in some direction may be desirable in various situations. Something close to 50 ohms impedance will aide matching and power transfer to/from coax cable.
There are many other potential goals for a dipole, but the ones I have listed are those that are most dependent on it's height above ground. Thus this discussion will not touch upon the issues of multi - banded operation, tuned open wire feeders, and the like. So, lets limit the issue at hand to: how the character of a dipole varies with its height above ground.
To investigate this problem, I have modeled a hypothetical wire dipole using the EZNEC program (from W7EL). This model is well within the verified capability of EZNEC.
For those interested in the modeling details, this dipole, named D40M, has the following specifications:
Material: #12 copper wire.
Length: 69.057 feet.
Ground Type: good (.005,13) NEC Sommerfield.
Frequency: 7.00 MHz nominal, but the comparative patterns were computed by adjusting the frequency slightly for resonance at each height.
The dipole was modeled at various heights from .05 wavelengths (7 feet) to 4 wavelengths (560 feet) above good ground. One may argue that 560 feet is ridiculous for a 40 meter dipole, but keep in mind that the data can be scaled down to a 10 meter dipole with similar results.
The table below tabulates the results. In the first two columns, the antenna's height above ground is given in wavelengths and in feet. The next two columns show the maximum gain in the favored direction (i.e. broadside to the wire), followed by the launch angle and the -3 dB vertical beam width. The next two columns once again present the gain and launch angle / beam width, but for the axial direction (off the ends of the wire). Finally, the last 2 columns list the complex impedance at the feed point, and the actual resonance frequency at that specific height.
| Height | Height | Fav Dir | Fav Dir | End Dir | End Dir | |||||
| Launch | Launch | |||||||||
| Wave | Gain | Angle/ | Gain | Angle/ | Feedpt | Res. | ||||
| Lengths | Feet | (dbi) | Bmwidth | (dbi) | Bmwidth | Z | Freq | |||
| 4.0* | 560 | 7.75 | 4 / 4 | 5.57 | 72 / 13 | 6.93 | ||||
| 3.0 | 420 | 7.83 | 5 / 5 | 5.25 | 68 / 14 | 77+ j11 | 6.94 | |||
| 2.0* | 280 | 7.80 | 7 / 7 | 0 | 39 / | 75 + j12 | 6.95 | |||
| 1.5 | 210 | 7.72 | 9 / 10 | -2.50 | 33 / | 75 + j11 | 6.96 | |||
| 1.0* | 140 | 7.64 | 14 / 15 | -11.00 | 20 / | 74 + j08 | 6.96 | |||
| .9 | 126 | 7.03 | 16 / 17 | -8.30 | 22 / | 85 + j13 | 6.94 | |||
| .8 | 112 | 7.16 | 18 / 19 | -6.40 | 25 / | 84 + j26 | 6.88 | |||
| .7* | 98 | 7.95 | 20 / 22 | -4.50 | 30 / | 70 + j30 | 6.88 | |||
| .6 | 84 | 8.35 | 23 / 26 | -1.95 | 40 / | 60 + j16 | 6.94 | |||
| .5* | 70 | 7.45 | 28 / 33 | -0.51 | 43 / 33 | 71 - j00 | 7.00 | |||
| .4 | 56 | 6.06 | 35 / 47 | 1.30 | 59 / 102 | 93 + j04 | 6.98 | |||
| .3* | 42 | 5.59 | 50 / 137 | 4.71 | 90 / 80 | 100 + j32 | 6.86 | |||
| .2 | 28 | 6.70 | 90 / 118 | 6.70 | 90 / 67 | 71 + j56 | 6.77 | |||
| .1* | 14 | 8.21 | 90 / 103 | 8.21 | 90 / 66 | 23 + j39 | 6.84 | |||
| .05 | 7 | 9.61 | 90 / 99 | 9.60 | 90 / 72 | 7 + j12 | 6.95 |
* Elevation plots shown below
The first thing to notice is that the gain in the favored (broadside) direction varies very little with height. The important change in the broadside pattern occurs in the launch angle of the primary lobe. As the antenna moves closer to the ground, the launch angle of radiation gets higher and the -3 dB vertical beam width becomes broader. Note that below the benchmark height of ½ wavelength, the launch angle increases rapidly. Once the dipole is lowered to 0.3 wavelengths, most of the radiation goes in a vertical direction. This explains the frequently heard "rule" that a dipole must be at least ½ wavelength high to work. The seeming anomaly with the beam width below 0.4 wavelengths is easier to understand by viewing the plots shown below.
One frequently sees a dipole azimuth pattern depicting a very sharp null off of the ends of a dipole. While technically accurate, this can be very misleading as the table above shows, and is a result of trying to depict a 3 dimensional pattern in 2 dimensions. This often seen null is only evident at the same launch angle as the maximum broadside gain. Of major significance is the large amount of gain off the ends at higher launch angles. Due to multiple lobes forming above ½ wavelength, this is not easily shown in tabular form. I have arbitrarily chosen to list gain and launch angle for the secondary lobe with the lowest launch angle, but recognize that there is frequently a stronger primary lobe at higher angles. Consult the plots below for a better visualization.
The reference antenna length was chosen to resonate at the ½ wavelength height. As expected, the feed point impedance oscillates significantly as the height changes from our reference point. Thus we verify the old adage that you must trim the dipole to fit your particular QTH (height being very important). The corresponding resonant frequency for each height is shown in the last column for reference, since complex impedance's may be of less practical importance to some.
Now we are back to looking at what we want the dipole to achieve.
For DX work, higher placement is warranted, since more power concentrated between 5 and 15 degrees is reported to be of major benefit. Heights around one wavelength are necessary to get the broadside lobe to launch in this range. However, higher may not always be better. Pay careful attention to the magnitude of secondary lobes in the broadside direction, as well as high angle radiation off the ends. Some heights would appear better than others due to concerns with nulling out local QRM. A complete discussion of of this aspect is beyond the scope of this article, but may be investigated at a later date.
For local work, lower heights appear to be more beneficial. Note especially how omni-directional our dipole becomes at lower heights. Below 0.4 wavelengths, there is less than 1 dB of attenuation in the end fire direction, which suggests a height between 0.4 and 0.3 might be an ideal compromise for local nets and rag chewing.
Feed point impedance and matching does not seem to be of major concern except at very low heights. The effect of height on 2:1 SWR bandwidth was not investigated.
Our first plot shows the elevation pattern in both the broadside (white trace) and end fire (yellow trace) directions for a height of 4 wavelengths, or 560 feet. Note the substantial high angle radiation in all directions, in addition to the excellent low angle lobes.
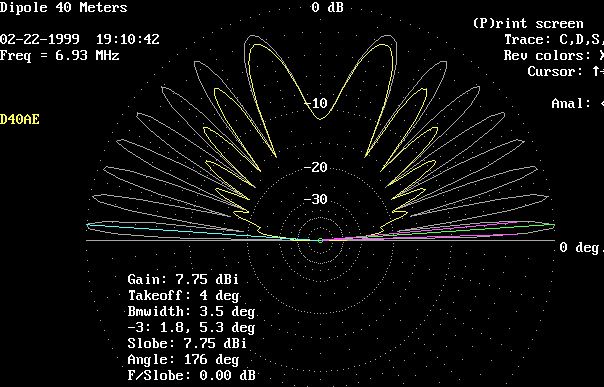
This plot shows the elevation patterns at a height of 2 wavelengths, or 280 feet.
White trace is broadside. Yellow trace is axial (off the ends).
Still Lots of high angle radiation.
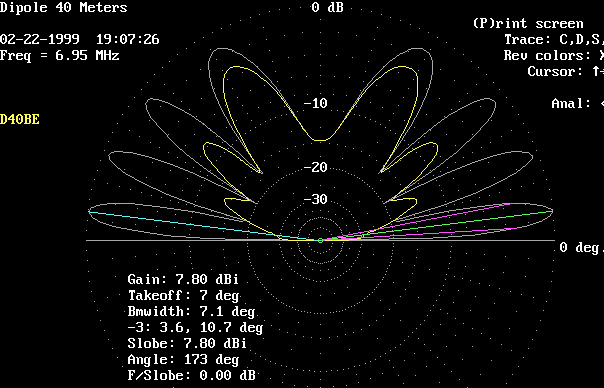
This plot shows the elevation patterns at a height of 1 wavelength, or 140 feet.
White trace is broadside. Yellow trace is axial (off the ends).
The secondary lobe is down to 47 degrees, but the primary lobe is up to 14 degrees.
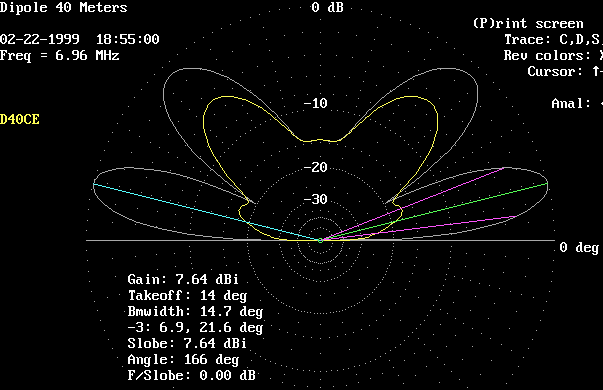
This plot shows the elevation patterns at a height of 0.7 wavelength, or 98 feet.
White trace is broadside. Yellow trace is axial (off the ends).
The primary lobe is up to 20 degrees.
Note the large vertical lobe which has appeared!
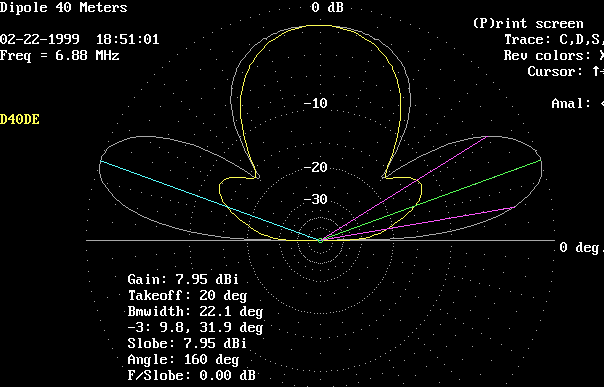
This plot shows the elevation patterns at a height of 1/2 wavelength, or 70 feet.
White trace is broadside. Yellow trace is axial (off the ends).
Now that's a classical dipole pattern!
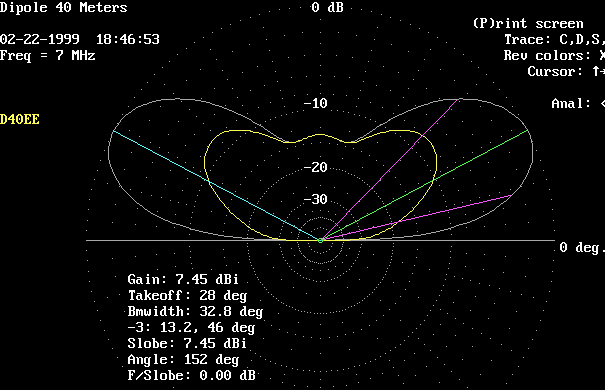
This plot shows the elevation patterns at a height of 0.3 wavelength, or 42 feet.
White trace is broadside. Yellow trace is axial (off the ends).
We are entering the "skywarmer" mode here.
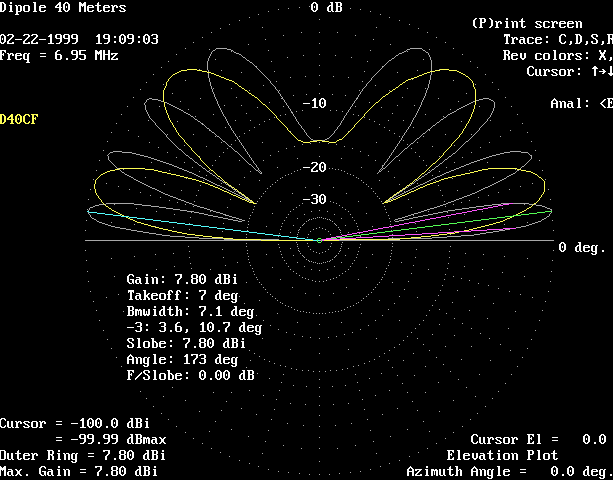
This plot shows the elevation patterns at a height of 0.1 wavelength, or 14 feet.
White trace is broadside. Yellow trace is axial (off the ends).
This plot shows comparative elevation patterns, in the broadside direction only,
White trace is for 2 wavelengths, 280 feet.
Yellow trace is for 1 wavelengths, 140 feet.
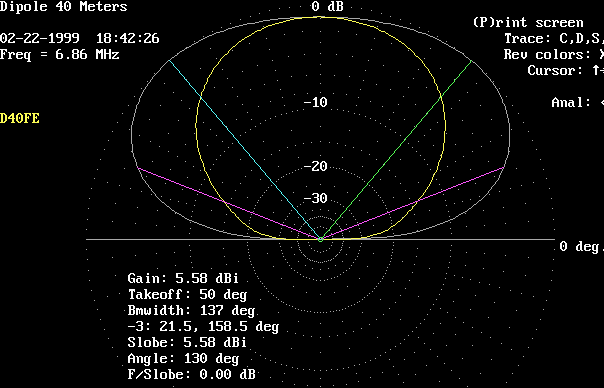
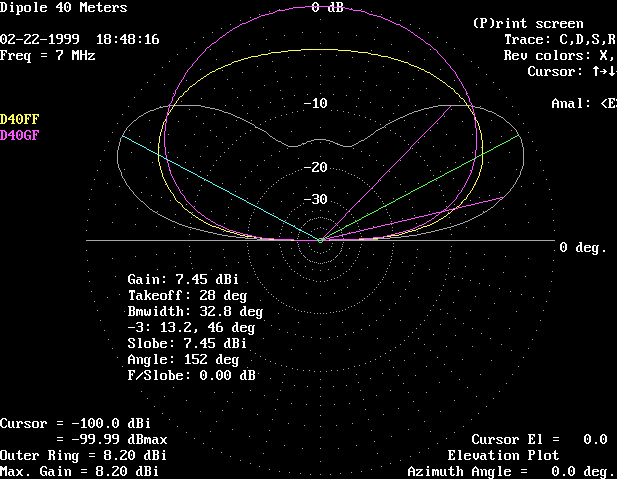
This plot shows comparative elevation patterns, in the broadside direction only.
White trace is for 0.7 wavelengths, 98 feet.
Yellow trace is for 0.5 wavelengths, 70 feet.
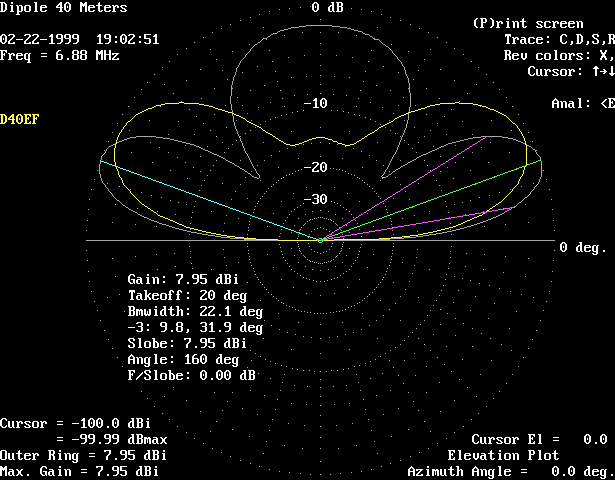
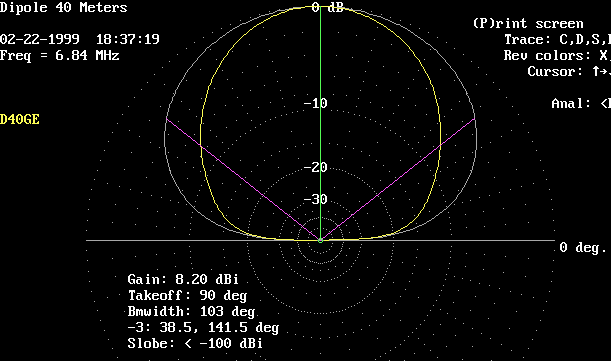
This plot shows comparative elevation patterns, in the broadside direction only.
White trace is for 0.5 wavelengths, 70 feet.
Yellow trace is for 0.3 wavelengths, 42 feet.
Pink trace is for 0.1 wavelengths, 14 feet.
Please distribute freely.
The author welcomes any questions, criticisms, or compliments via email.
File.
ant2.rtf
ant2.html